

Peaking into the Why of Pi: A Further Look
Dive deeper into π this Pi Day with Mister Marx! Join Mister Marx on a captivating journey beyond the familiar 3.14, as we unravel π's profound story through a newly illustrated animated GIF. From its fundamental role in mathematics to its presence in the real world, discover how this number continues to fascinate and inspire. Are you ready to explore the infinite mysteries of π and its impact on our understanding of things? Click to uncover the wonders waiting. Happy π Day!

Mister Marx Math Adventures #012 | Algebra I | Demystifying ‘f(x)’ Function Notation & The Magic of Inputs & Outputs
In Episode #012 of 'Mister Marx Math Adventures', we're embarking on a thrilling journey to demystify the concept of 'f(x)' in mathematics. Imagine a magical machine that transforms numbers and concepts right before your eyes – this is the kind of adventure we're diving into! Perfect for both math enthusiasts and those just a tad curious about algebra, this episode is designed to unravel the complexities of function notation in a fun, engaging, and highly visual manner.

Mister Marx Math Adventures #011 | Algebra I | Dividing by Zero and Infinite Growth Rate?
Join me as Mister Marx as a business marks its first anniversary with an exploration into Algebra I! In Episode #011, we delve into the curious concepts of Dividing by Zero and Infinite Growth Rate. This episode is a treat for both math aficionados and curious minds eager to expand their mathematical horizons. Dive into the latest blog post and join the mathematical adventure with Mister Marx – where every episode is not just a lesson, but an exploration into the fascinating world of math! 🎉📚🤓

Mister Marx Math Adventures #010 | Algebra I | Box Method for Multiplying Binomials
Dive into the fascinating world of algebra with Mister Marx Math Adventures! In Episode #010, we unlock the secrets of multiplying binomials through the visually stimulating Box Method. This episode is an extension of my blog post "Box It Up: The Simple Solution to Multiplying Polynomials". Join me as we engage in interactive problem-solving, animated visual learning, and explore the intriguing patterns in binomial multiplication. Whether you're a math enthusiast or a curious learner, this adventure is tailored to transform the way you see and understand mathematics. Get ready to visualize, discover, and engage with math like never before! 📚✨🧮

*NEW* Mister Marx Math Adventures Companion Worksheet | *FREE* TPT.com Resource
Dive into the world of numbers with Mister Marx Math Adventures like never before with the latest FREE Mister Marx TPT.com Store release - the Mister Marx Math Adventures Companion Worksheet! This free, innovative tool is designed to boost how students interact with Mister Marx Math Adventures on YouTube, turning each lesson into a fun, active-learning quest for knowledge. Ready to transform math into an adventure? Click now to get all the details on how to maximize this engaging new resource in your classroom.

Mister Marx Math Adventures #009 | Algebra I | Area Model for Multiplying Binomials
🌟 Dive into the world of algebra with Mister Marx Math Adventures #009! Today, we're unraveling the secrets of multiplying binomials in a way you've never seen before. Using the Area Model, we transform complex algebraic concepts into a colorful, visual journey. Witness blocks of colors come together to form the story right before your eyes, turning complex ideas into tangible patterns. Join us in this latest episode to not only learn but visually experience the art of algebra. Are you ready to see math in a new light? Click to read the full blog post and embark on a mathematical adventure with Mister Marx! 🎨🔢

Mister Marx Math Adventures #008 | Algebra I | Graphs & Table of Values
Embark on another exciting journey with Mister Marx in Episode #008 of Math Adventures, where we revisit the intriguing plant growth problem from Episode #004 with a new perspective – through the lens of graphing! Uncover the secrets of intersection points, visualize the growth trajectories, and embrace the power of Mathematical Representations. Join me as we plot our way to understanding!

Mister Marx Math Adventures #007 | Algebra I | Linear Equations & Multiple Choice
Join Mister Marx in Episode #007 of Math Adventures as we delve into the wonders of Linear Equations. Explore y-intercepts, slopes, and transition to slope-intercept form. Enhance your analytical reasoning and critical thinking with algebraic concepts. Let's make math fun together!

The Power of Pascal’s Triangle: Exploring Mathematical Patterns
Are you ready to explore a major source of patterns - Pascal’s Triangle? 🚀 Discover the patterns and structures of this fundamental mathematical concept using an animated GIF that makes it easy to understand & interact with. Even if you have zero prior knowledge of Pascal’s Triangle, you can still engage and discover its many secrets. Don't miss out on this fun & interactive way to explore & learn about Pascal’s Triangle!

Comment Chronicles: Multiplying Polynomials With The Carve Copy Distribute (CCD) Method
Dive into the world of the Carve Copy Distribute Method for polynomial multiplication, introduced by an innovative member of our community. In my latest Comment Chronicles series, take a dive into this approach whose versatility shines. Intrigued? Click to learn the CCD Method and level up your math prowess!

From Ants to Galaxies: Visualizing Infinity on Pi Day
Greetings, fellow math enthusiasts! As we celebrate Pi Day, I couldn't help but ponder the concept of infinity - a topic that has fascinated mathematicians for centuries. From the vast expanse of the universe to the perspective of an ant on a never-ending highway, contemplating infinity challenges our minds to think beyond the limits of everyday experiences. Join me on a journey to unlock the mysteries of pi and explore the boundless concept of infinity. Let's challenge our thinking and discover new ways to enjoy math together.

Visually Tackle Basic Multiplication with the Area Model
Journey into the world of basic multiplication with the area model. This visual method utilizes colored blocks to perform basic multiplication, allowing patterns to emerge & the process to become easier to understand. Explore the patterns & structures in the arrangement of the colored blocks, how they relate to the math, & how they interact to create the final product. Embrace your curiosity & have fun with this colorful journey.

Math Battle: #FOIL vs #AreaModel vs #BoxMethod - Multiplying Binomials
📣 Are you Team #FOIL, Team #AreaModel, or Team #BoxMethod when it comes to multiplying binomials? Vote for your favorite by 'Liking' this blog post & sharing. Don’t forget to share your thoughts in the comment section below!
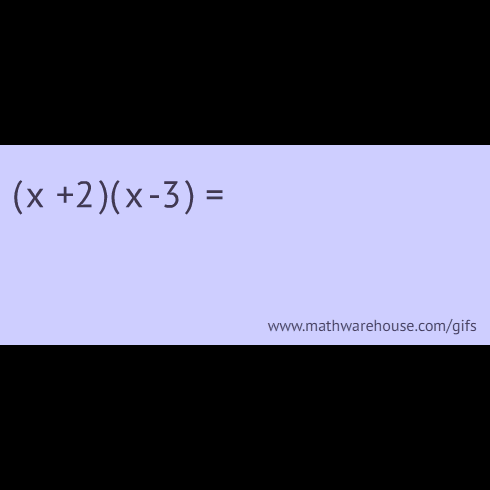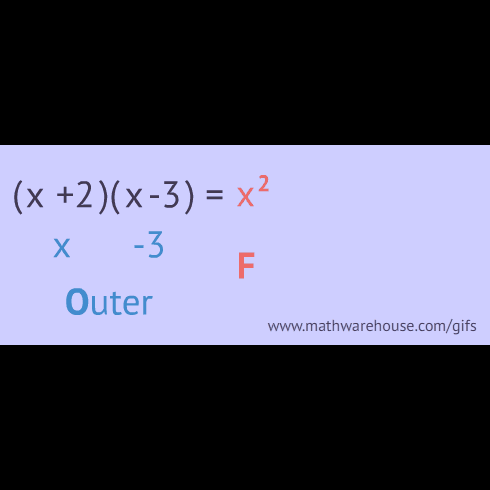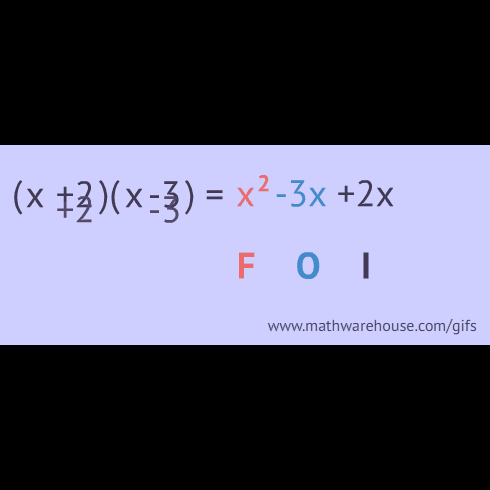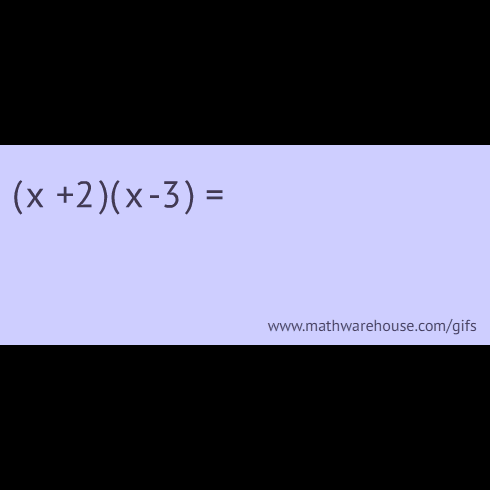
FOIL’ing through Math: A Blast from the Past!
Take a trip down memory lane to explore the classic FOIL method for multiplying binomials. Is FOIL still relevant in today's mathematics education? Or is FOIL something to be left in the past? Don't miss out on this opportunity to learn about Mister Marx's perspective on this topic & to find out what you can learn about this #Throwback method.
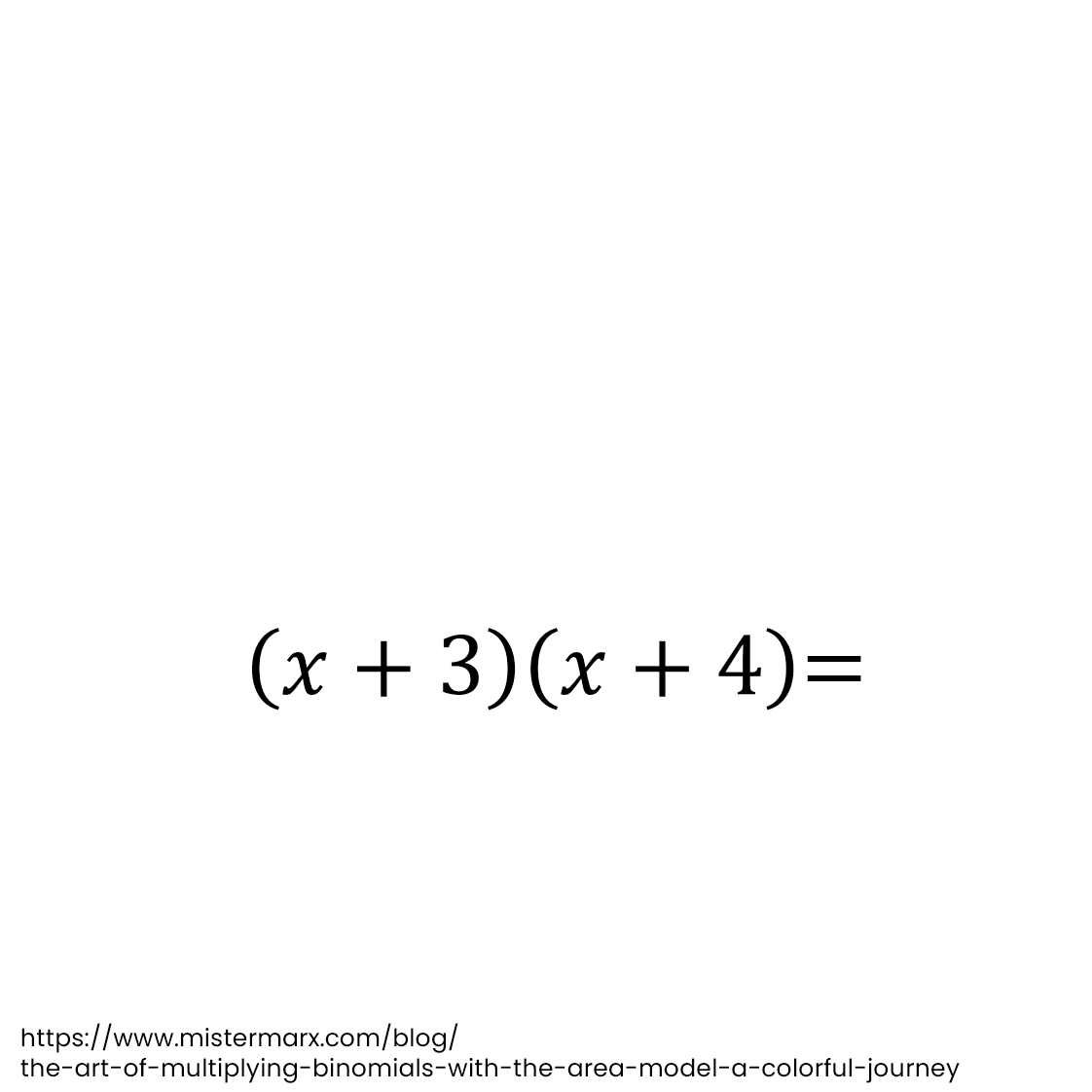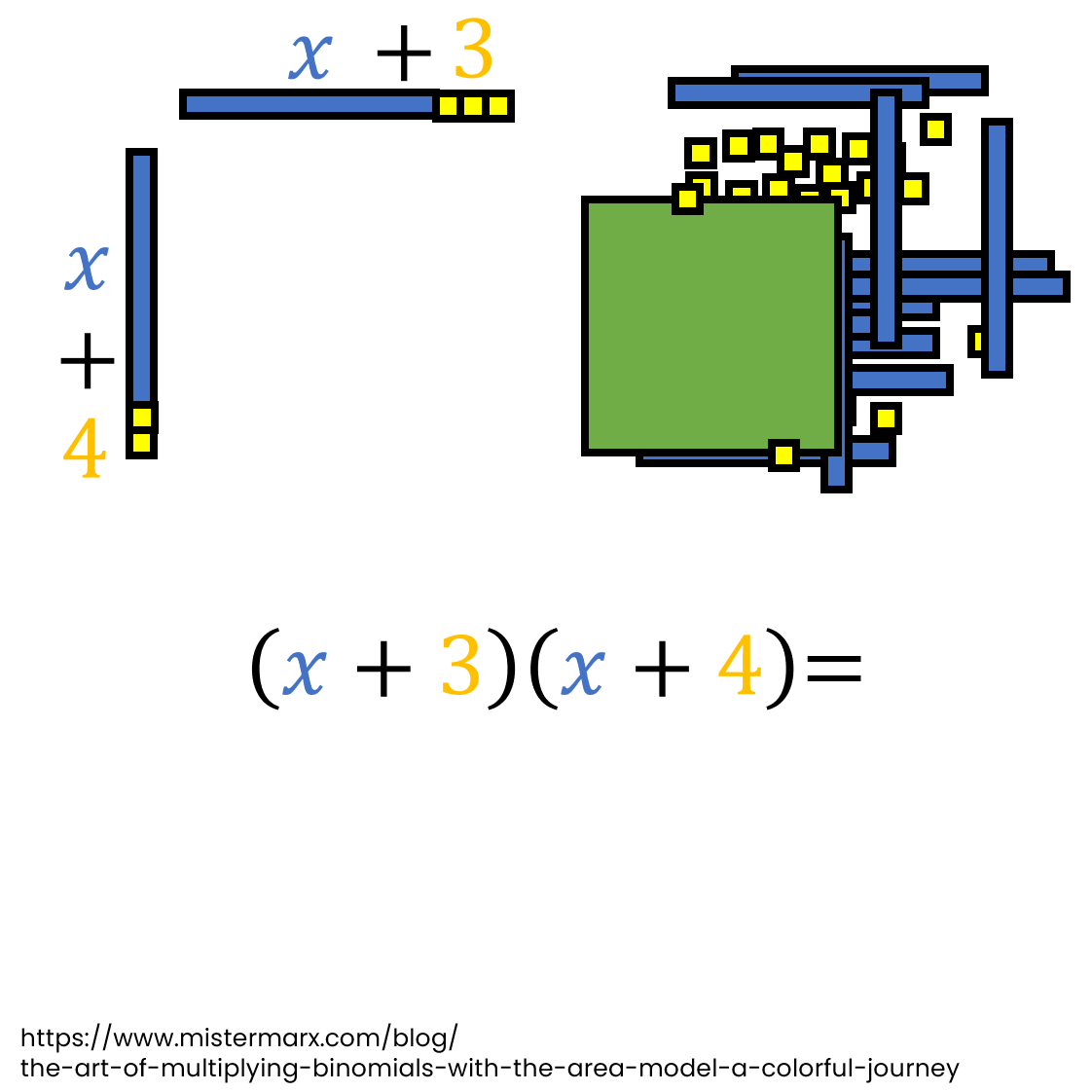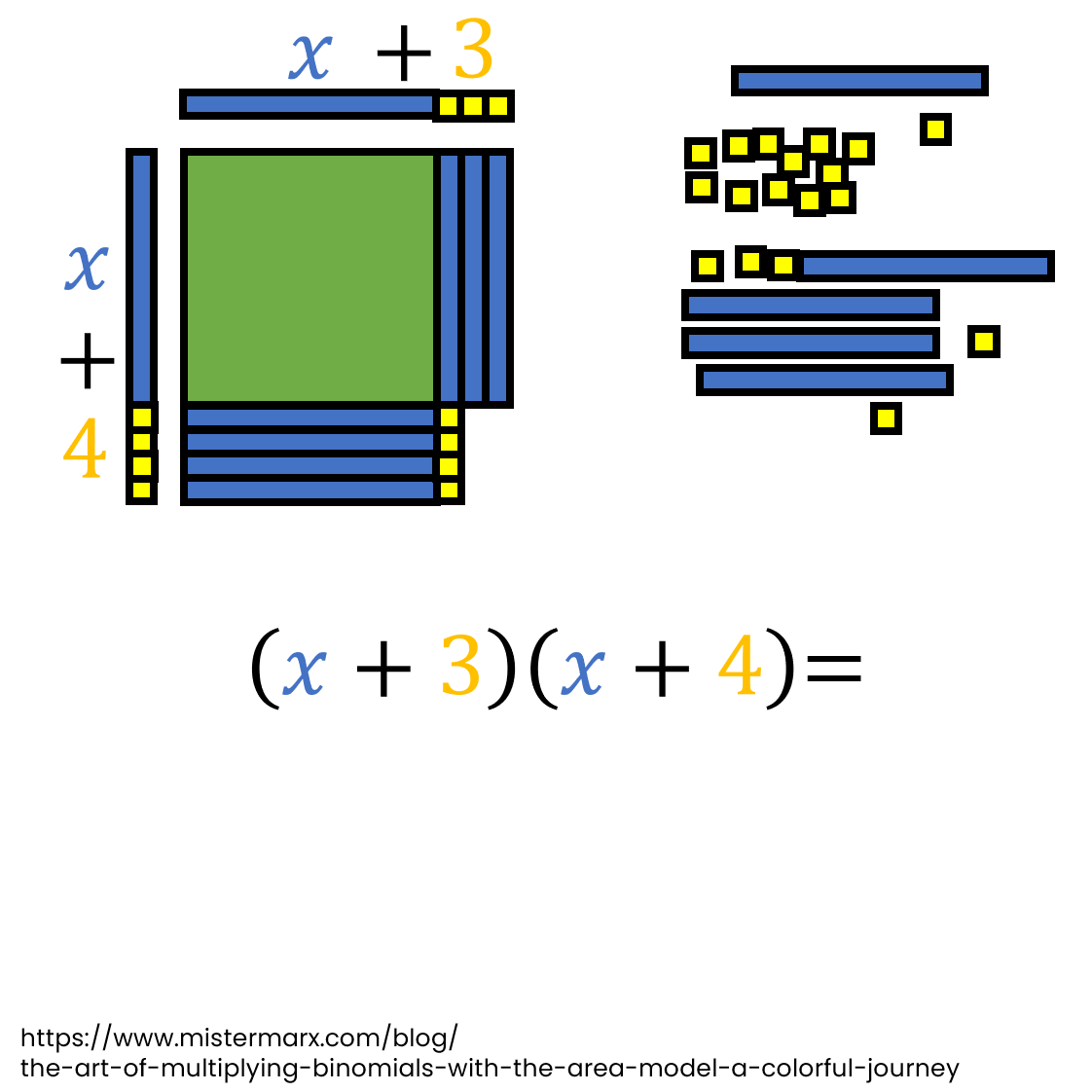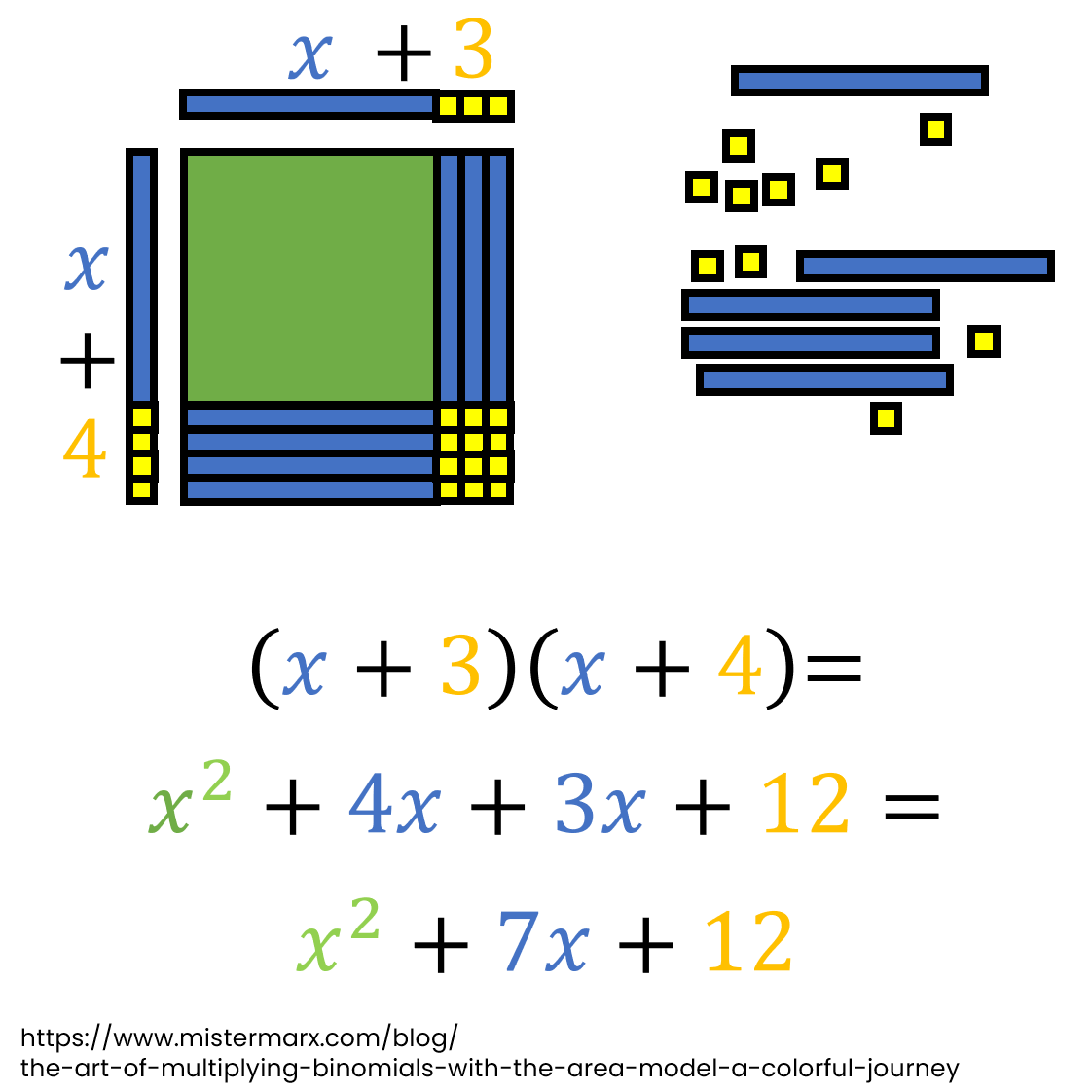
The Art of Multiplying Binomials with the Area Model: A Colorful Journey
Dive into the world of multiplying binomials with a fun & colorful journey! The area model is a visually appealing method that makes understanding the process of multiplying binomials easy. Experiment, have fun, & witness patterns emerge as we animate the multiplication of two binomials. Click to embark on this colorful journey now!

Box It Up: The Simple Solution to Multiplying Polynomials
Unleash the power of simplicity in multiplying polynomials with the box method! In this post, we'll learn a fun, easy way to multiply polynomials without diving too deep into the math. Get organized & multiply polynomials without losing any terms with the help of the box method. Join us on this journey to foster curiosity & the desire to discover!
As part of Mister Marx's /Power Pair Series/, this post pairs with “Factor This! Breaking Down Quadratics with the Box Method”! to highlight the versatility of the box method.

Factor This! Breaking Down Quadratics with the Box Method
Unravel the mystery of factoring quadratics with the Box Method! This step-by-step guide teaches you a simple & fun way to turn polynomials into their factors without losing track of any terms. Discover how the Box Method helps you visually organize the problem & keep track of all the parts as you factor. Whether you're a math newbie or a seasoned pro, join us on this journey of discovery & expand your knowledge with the Box Method.
As part of Mister Marx's /Power Pair Series/, this post pairs with “Box It Up: The Simple Solution to Multiplying Polynomials”! to highlight the versatility & power of the box method.
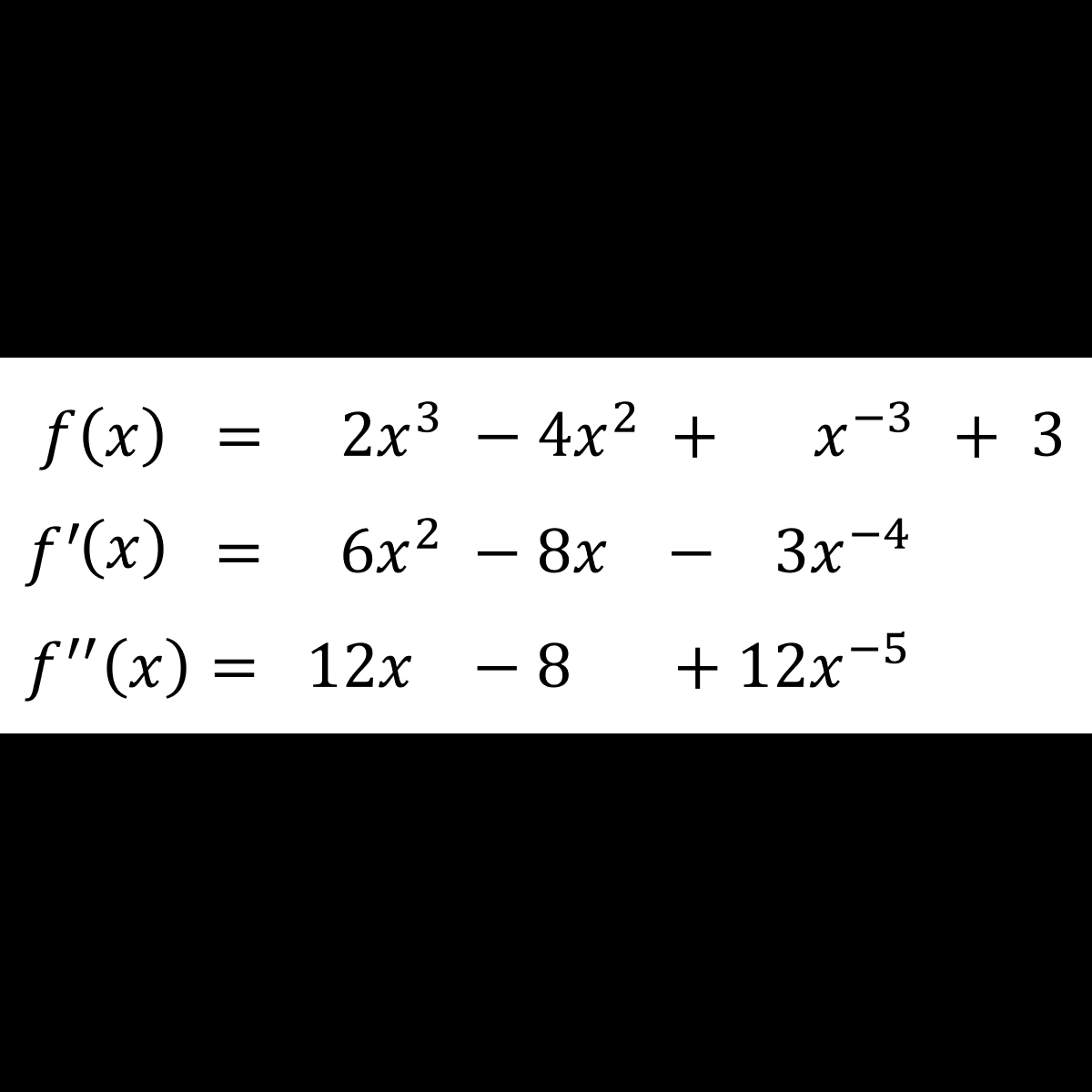
Understanding Change: Peer Into the World of Calculus
Be bold & engage with an interactive introduction to the concept of derivatives in calculus. Use three equations to anchor an exploration that will leave you equipped with a few new pieces of calculus knowledge. Click now to read my full post & learn about the power of derivatives!

The Magic of Binomial Expansions: A 3D Experience in Structure & Patterns
Are you ready to take a visual journey through the world of binomial expansions? 🚀 Explore the patterns and structures of this fundamental mathematical concept using 3D visualizations that make it easy to understand & interact with. Even if you have zero prior knowledge of algebra, you can still engage and discover the secrets of binomial expansions. From the first expansion all the way to the third power, you will be asking questions & encouraging yourself to think differently. Don't miss out on this fun & interactive way to learn about binomial expansions!

A Glimpse into the Fascinating World of Trig Functions: No Math Degree Required
The Trig Functions sin(θ) and cos(θ) are important aspects of mathematics and science. They play a crucial role in navigation, physics, and engineering. But where do these functions come from? One way to understand their origins is through the lens of circles. By observing the movement of a point tracing around the circumference of a circle, we can see how it is connected to the creation of both the sin(θ) and cos(θ) curves. This is a fascinating concept, and one that can be explored by anyone, regardless of their math knowledge.