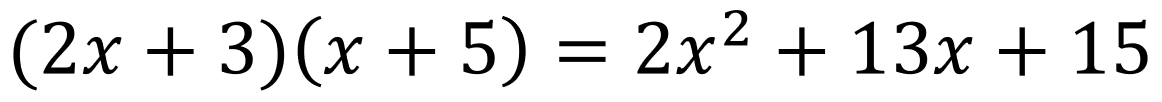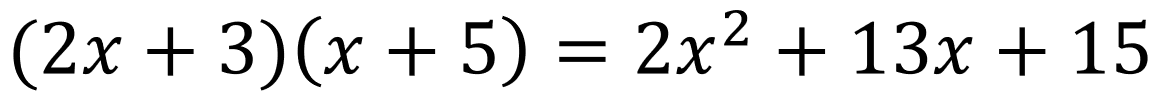Box It Up: The Simple Solution to Multiplying Polynomials
The Box Method: A Step-by-Step Guide to Multiplying Polynomials
UPDATE: This blog post was featured in Episode #010 of #MisterMarxMathAdventures on YouTube.
Catch that latest blog post here: 🔗 https://www.mistermarx.com/blog/mister-marx-math-adventures-010-multiplying-binomials-with-the-box-method 🔗
Or watch the full episode over on YouTube: 🔗 https://youtu.be/U9LAOEUBexk 🔗
Multiplying polynomials can seem confusing at first, but don't worry! There's a simple & easy-to-follow method called the box method that can help you get the hang of it. With this post, we are not going to dive too deep into the mathematics, but instead are going to learn a fun, simple way to multiply polynomials using the box method. So regardless of your prior history with math, I hope you choose to take a look at the box method with me & enjoy learning some math today!
(2x+3) & (x+5) are both polynomials.
These polynomials can be multiplied in order to produce the polynomial on the right side of the equation. But how? Well, there are many ways to organize multiplying polynomials like this.
One of my favorite ways to visually organize how to multiply polynomials like this is called the box method. Let’s walk through the steps to multiply polynomials with our example polynomials from earlier.
To get started, draw a large box. Inside that large box, draw four smaller boxes arranged in two rows & two columns.
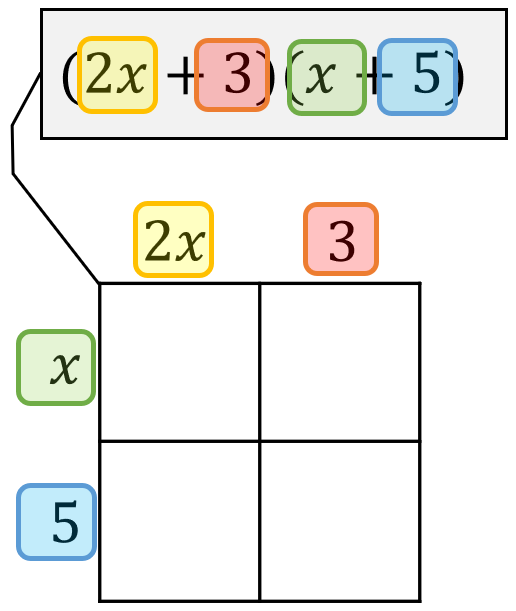
Next, write each term of (2x+3) along the top: 2x above the first column & 3 above the second column. Similarly, write each term of (x+5) along the left: x to the left of the first row & 5 to the left of the second row.
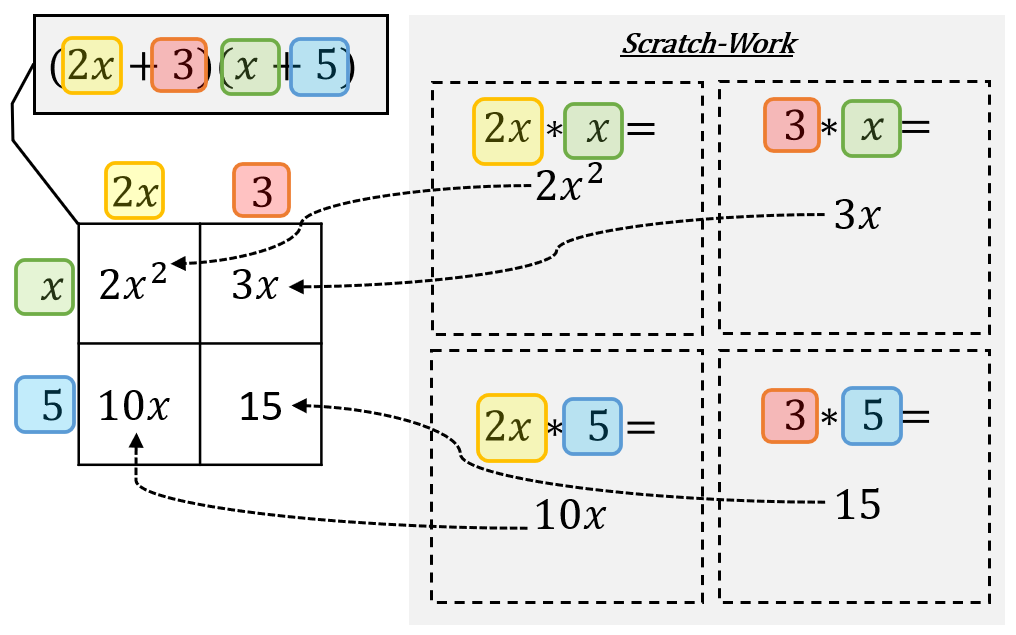
Now, for each small box, multiply its column value by its row value.
Finally, combine the four terms in your boxes & simplify - that’s it!
& just like that, we have successfully used the box method to multiply polynomials. The box method helps you to organize the problem at hand & keep track of all of the parts as you perform the multiplication. By using the box method, you are empowered with the ability to multiple polynomials without losing any terms! Remember, the aim of this journey was not to find the perfect answers, but to foster curiosity & the desire to discover; so don't be afraid to think differently & challenge yourself. Until next time, keep exploring & keep learning!
Want more practice multiplying polynomials with the box method? Check out My TPT.com Resource: (Coming Soon).
Want more box method but in the opposite way? (What does that even mean?) Check out Factor This! Breaking Down Quadratics with the Box Method.
Further Questions to Ponder:
Does using the box method like this ever not work? How can you figure that out?
Does this method work for different types of polynomials, such as those with more than four terms? (2x³+3x²-4x+1)(x²-2) for example?
What other ways can multiplying polynomials be visualized? (Stay tuned to Mister Marx’s Math Corner for more!)
This post is part of Mister Marx’s Power Pair Series of blog posts. Box It Up: The Simple Solution to Multiplying Polynomials pairs with Factor This! Breaking Down Quadratics with the Box Method. Together, the pair of blog posts highlight the various ways the box method can be used.